Contents

TAREA MATLAB

%Tarea por Laura Priscila Abascal Pachito
%Semana del 3/1 al 15/1 de 2019
%Asignatura de Computación Aplicada a la Ingeniería
%Grado en Tecnologías Industriales

EJERCICIO 1. Curva de Bézier

Apartado a) Cálculo del factorial recursivo

%La función definida es la siguiente:
% function f = factr(n)
% if n == 0
%     f = 1;
% else
%     f = n * factr(n-1);
% end
% end

n=3;%Los puntos de control que se dan en el enunciado son 4 (n+1)
factorial=factr(n)

factorial =

     6

Apartado b) Función combina

%La función definida es la siguiente:
% function f = combina(n,j)
% %n:tamaño de la colección
% %j:vector de cero a n
% a=n-j;
% f=factr(n)/(factr(j)*factr(a));
% end

n=3;%Los puntos de control que se dan en el enunciado son 4 (n+1)
%j=input('Indica el valor de i entre 0 y n: ');
j=2;%Por ejemplo
combinacion=combina(n,j)

combinacion =

     3

Aparatado c) Polinomio de Bernstein

%La función bernstein desarrollada es:
% function f=bernstein(n,t)
% %Parámetro t, según se indica en el enunciado está en el intervalo [0,1]
% coef=[];
% for i=0:n
%     comb=combina(n,i);
%     a=n-i;
%     b=comb*t^i*(1-t)^a;
%     coef=[coef b];
% end
% f=coef'; %Muestra vector con los valores que toma el polinomio
% end
n=3;%Los puntos de control que se dan en el enunciado son 4 (n+1)
%t=input('Indica un valor que esté dentro del intervalo [0,1]: ');
t=0.4;%Por ejemplo
polinomio=bernstein(n,t)
% Función para el dibujo de los polinomios de grado 3 de Bernstein:
% function f=ber_vect(n,t)
% %Función que recurre a bernstein para dibujar los valores de los polinomios
%en la misma gráfica
%b=bernstein(n,t);%Vector con los valores del polinomio para un t
% m=length(t);
% b=[];
% for j=t
%    b1=bernstein(n,j);
%    b=[b b1];%Se guardan todos los valores de los polinomios
%    plot(j,b1,'o');hold on
%
% end
% grid on, title('Gráfico de valores los polinomios de bernstein de grado n');
% xlabel('Parámetro t');ylabel('Valores');
% hold off
% figure(2)
% plot(t,b);grid on,title('Gráfico de los polinomios de bernstein de grado n');
% xlabel('Parámetro t');
% end
%Ejemplo:
t1=0:0.1:1;
ber_vect(n,t1);

polinomio =

    0.2160
    0.4320
    0.2880
    0.0640

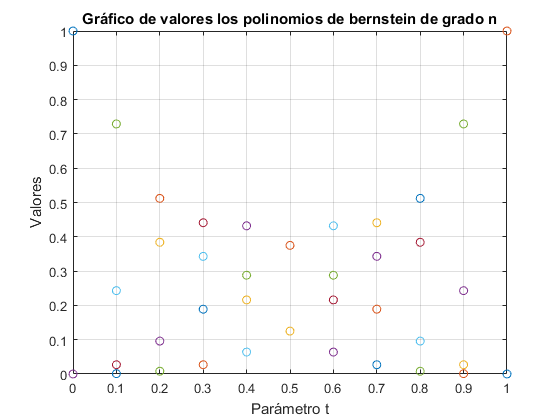
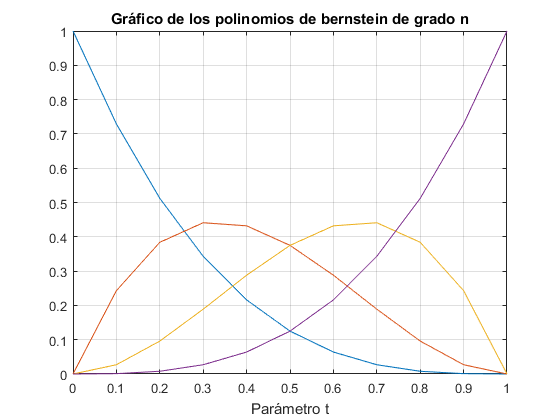
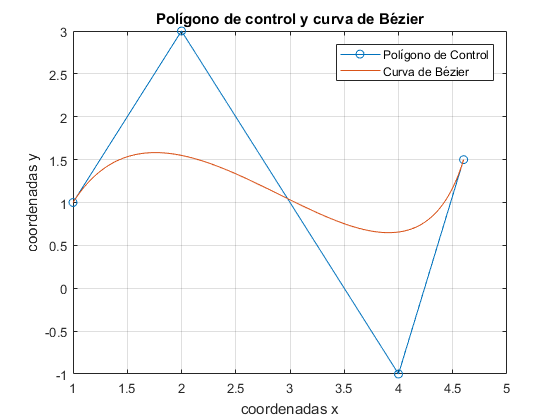
Apartado d) Gráficas del polígono de control y la curva de Bézier

%Vectores:(de dos componentes: la curva es planar, por tanto)
vx=[1 2 4 4.6]';
vy=[1 3 -1 1.5]';
%Variación del parámetro t en 0.01
t=0:0.01:1;
%Representación del polígono de control:
figure(3)
plot(vx,vy,'-o');grid on, hold on;
title('Polígono de control y curva de Bézier'); xlabel('coordenadas x');ylabel('coordenadas y');
n=3;
%Por cada t se tiene un punto de coordenadas x,y
X1=[];Y1=[];
for j=t
    b=bernstein(n,j);
    x1=vx.*b;
    y1=vy.*b;
    %Vectores que guardan los valores de la curva de Bézier para cada i:
    X1=[X1 x1];
    Y1=[Y1 y1];
end
%Para guardar en un vector todos los valores de los sumatorios para cada t:
xx=[];yy=[];
for j=1:length(X1)
    xx=[xx;sum(X1(:,j))];
    yy=[yy;sum(Y1(:,j))];
end
plot(xx,yy);hold off
legend('Polígono de Control','Curva de Bézier');

Ejercicio 2. Velocidad de viento y potencia del aerogenerador

Apartado a) Lectura de datos y gráfico del histograma

lect1=xlsread('sotaventogaliciaanual.xlsx');
int1=0:25;
%Histograma:
figure(1)
hist(lect1(:,1),int1);grid on
title('Histograma 1');

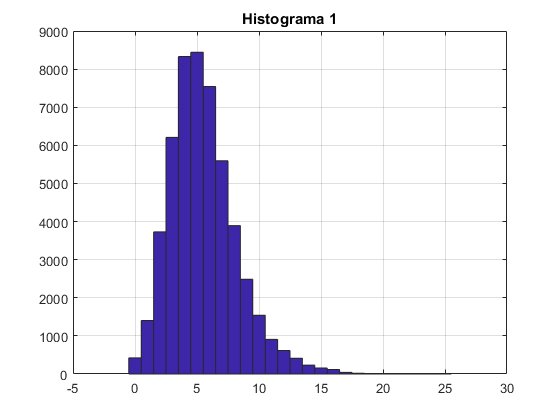
Apartado b) Lectura de datos, gráfico del histograma de frecuencias y ajuste de Weibull

%Lectura de datos:
lect1=xlsread('sotaventogaliciaanual.xlsx');
velocidad=lect1(:,1);

%Interpolación si necesario
if any(isnan(velocidad)) %si hay algún NaN
    x=1:length(velocidad);
    i=find(~isnan(velocidad));
    velocidad=interp1(x(i),velocidad(i),x);
end

%Histograma
x=0.5:1:max(velocidad);
horas=hist(velocidad,x);
%Convierte a frecuencias
frec=horas/sum(horas);

%Ajuste a la función de Weibull
modelfunc=@(a,x) (a(1)/a(2))*((x/a(2)).^(a(1)-1)).*exp(-(x/a(2)).^a(1));
beta0=[mean(velocidad) std(velocidad)];%Valores iniciales de los parámetros
beta=nlinfit(x,frec,modelfunc,beta0);
%Gráfica del ajuste

%diagrama de frecuencias
figure(2)
bar(x,frec,'b');grid on;hold on
%representa la curva de ajuste
x=linspace(0,max(velocidad),100);
y=modelfunc(beta,x);
plot(x,y,'r')
title('Ajuste a la función Weibull')
xlabel('Velocidad')
ylabel('Frecuencia')
hold off

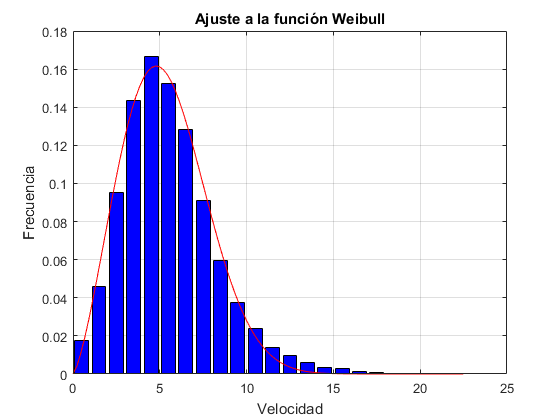
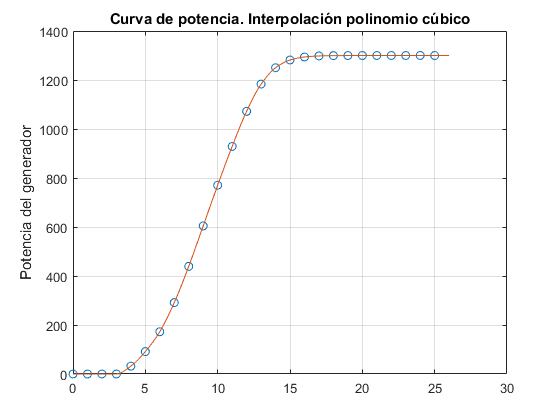
Apartado c) Interpolación de la curva de poencia del aerogenerador

%Lectura de los datos de la curva
lect2=xlsread('sotavento_curva potencia.xlsx');
x = lect2(:,1);
y = lect2(:,2);
n=length(x);
xx = linspace(0, n);
y1=interp1(x,y,xx,'pchip');
figure(3)
plot(x, y, 'o', xx, y1, '-');grid on;title('Curva de potencia. Interpolación polinomio cúbico')
ylabel('Potencia del generador')

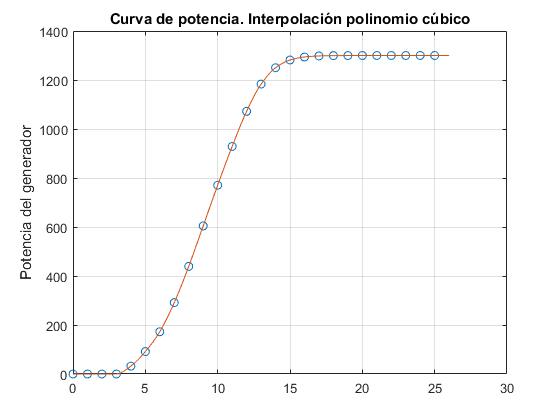
Apartado d) Script que agrupa los dos apartados anteriores e introduce la integración por quad

%Lectura de datos:
lect1=xlsread('sotaventogaliciaanual.xlsx');
velocidad=lect1(:,1);

%Interpolación si necesario
if any(isnan(velocidad)) %si hay algún NaN
    x=1:length(velocidad);
    i=find(~isnan(velocidad));
    velocidad=interp1(x(i),velocidad(i),x);
end

%Histograma
x=0.5:1:max(velocidad);
horas=hist(velocidad,x);
%Convierte a frecuencias
frec=horas/sum(horas);

%Ajuste a la función de Weibull
modelfunc=@(a,x) (a(1)/a(2))*((x/a(2)).^(a(1)-1)).*exp(-(x/a(2)).^a(1));
beta0=[mean(velocidad) std(velocidad)];%Valores iniciales de los parámetros
beta=nlinfit(x,frec,modelfunc,beta0);

%Gráfica del ajuste
%diagrama de frecuencias
figure(4)
bar(x,frec,'b');grid on;hold on
%representa la curva de ajuste
x=linspace(0,max(velocidad),100);
y=modelfunc(beta,x);
plot(x,y,'r')
title('Ajuste a la función Weibull')
xlabel('Velocidad')
ylabel('Frecuencia')
hold off
%Lectura de los datos de la curva
lect2=xlsread('sotavento_curva potencia.xlsx');
x = lect2(:,1);
y = lect2(:,2);
n=length(x);
xx = linspace(0, n);
%Interpolaión de la curva de potencia del generador:
y1=interp1(x,y,xx,'pchip');%Polinomio cúbico
figure(5)
plot(x, y, 'o', xx, y1, '-');grid on;title('Curva de potencia. Interpolación polinomio cúbico')
ylabel('Potencia del generador')

k=beta(1);c=beta(2);
%POTENCIAS:
%Directamente de los datos de las velocidades del viento
potencia=0.5*1.225*sum(velocidad.^3)/length(velocidad);
fprintf('Potencia, directamente de las medidas: %3.1f\n',potencia);
media=mean(velocidad);
%Usando la función gamma para el ajuste de Weibull
media=mean(velocidad);
potencia=0.5*1.225*media^3*gamma(1+3/k)/(gamma(1+1/k)^3);%Función de distribución de Weibull
fprintf('Potencia, función Weibull: %3.1f\n',potencia);
%Potencia media con quad
%Datos:
Pr=1300; x0=4.0;xr=20;x1=25;
potencia=xlsread('sotavento_curva potencia.xlsx','B2:B27');
x=0:1:25;
pot=potencia(x>=x0 & x<=xr);
x=x0:1:xr;
%Ajuste
p=polyfit(x,pot',3); %ajuste a un polinomio de tercer grado
yp=polyval(p,x);
%cálculo de la potencia media
f=@(x) (k/c)*((x/c).^(k-1)).*exp(-(x/c).^k); %función de Weibull
h=@(x) f(x).*polyval(p,x);
power=quad(h,x0,xr);
fprintf('La potencia media es: %3.1f\n',power)

Potencia, directamente de las medidas: 187.8
Potencia, función Weibull: 170.0
La potencia media es: 199.1

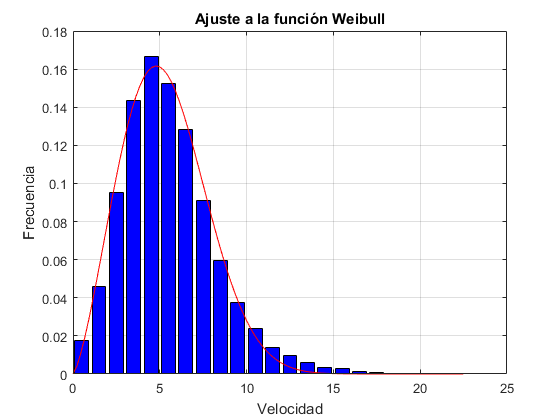
EJERCICIO 3. Movimiento de un sistema masa-resorte-amortiguador

%Datos del enunciado
%Masa:
m=20;
%Constante del resorte:
k=20;
%Posición y Velocidad iniciales:
xv0=[1,0];
%Para una período de 40s:
tf=40;
%Coeficientes de amortiguamiento dados:
c1=5;
c2=40;
c3=200;

%Una función por cada coeficiente de amortiguamiento:
f1=@(t,x) [x(2);(-k*x(1)-c1*x(2))/m];%c=5
f2=@(t,x) [x(2);(-k*x(1)-c2*x(2))/m];%c=40
f3=@(t,x) [x(2);(-k*x(1)-c3*x(2))/m];%c=200

%Resolviendo mediante el solver de RKF45
[t1,x1]=ode45(f1,[0,tf],xv0);
[t2,x2]=ode45(f2,[0,tf],xv0);
[t3,x3]=ode45(f3,[0,tf],xv0);

%Representaciones gráficas:
plot(t1,x1(:,1),t2,x2(:,1),t3,x3(:,1));grid on
xlabel('t(s)');
ylabel('x(m)');
title('Sistema Masa-Resorte-Amortiguador');
legend('c=5','c=40', 'c=200');

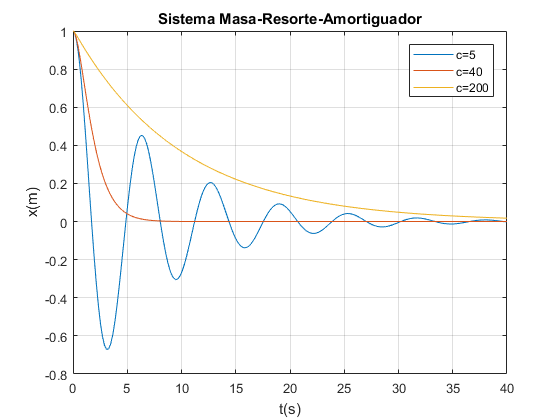
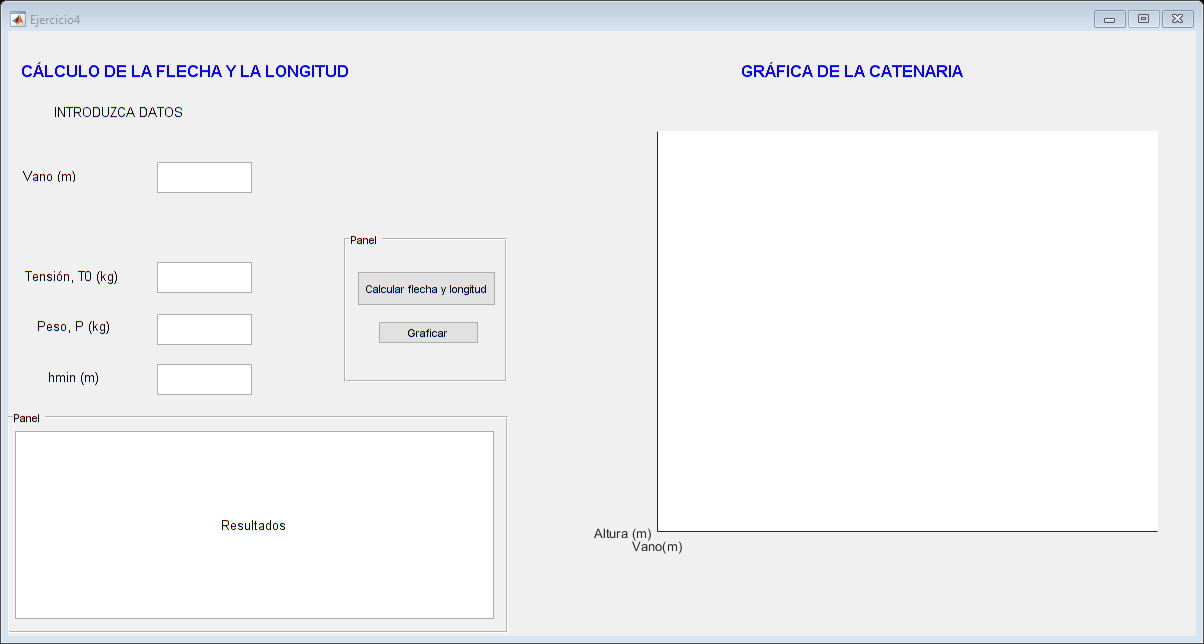
EJERCICIO 4. GUI. Cálculo de la flecha y la longitud así como representación de la catenaria

Ejercicio4

Published with MATLAB® R2017a